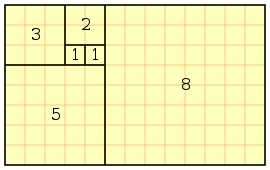
Ciąg liczb nazywany ciągiem Fibonacciego tworzą liczby naturalne powstałe z sumy dwóch poprzedzających je wartości.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610 …
Dla przykładu liczba 5 powstała poprzez dodanie 2 i 3, liczba 8 to suma 5 i 3, 13= 8+5 itd. Jeśli będziemy dzielić kolejne liczby w sekwencji przez liczby występujące przed nimi okazuje się, że za każdym razem otrzymamy wynik oscylujący wokół niewymiernej wartość 1,61803398875….. np. 21 podzielone przez 13 daje w przybliżeniu 1,618.
Dzielenie liczb z ciągu przez liczbę następną daje nam wartość 0,618…, czyli 13 podzielone przez 21 da mam w przybliżeniu 0,618. 0,618 jest więc odwrotnością 1,618.
Współczynnik 1,618033…. w średniowieczu został nazwany boską proporcją. Współcześnie spotyka się głównie dwie nazwy: złoty podział lub złoty środek. W algebrze oznacza się go grecką literą phi ɸ = 1,618.
Współczynnik 1,618033…. w średniowieczu został nazwany boską proporcją. Współcześnie spotyka się głównie dwie nazwy: złoty podział lub złoty środek. W algebrze oznacza się go grecką literą phi ɸ = 1,618.

Stosunek co drugiej liczby w ciągu Fibonacciego odkrywa przed nami kolejne współczynniki. Dzieląc 3 przez 8 otrzymamy wartość przybliżoną do 0,382. jeśli 8 podzielimy przez 3 otrzymamy w przybliżeniu 2,618. Postępując analogicznie w co trzecią wartością ciągu otrzymamy: 0,236 i 4,236.

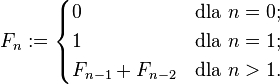
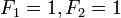
 ciągu Fibonacciego to:
ciągu Fibonacciego to:
 --
--